虚数i的运算公式及应用领域解析（揭开虚数i的神秘面纱，探索其运算公式及应用领域）

虚数i是数学中的一个重要概念，它在解决一些实际问题时起到了关键作用。本文将深入探讨虚数i的运算公式及其在不同领域的应用，希望读者通过本文的阅读能够对虚数有更深刻的认识。

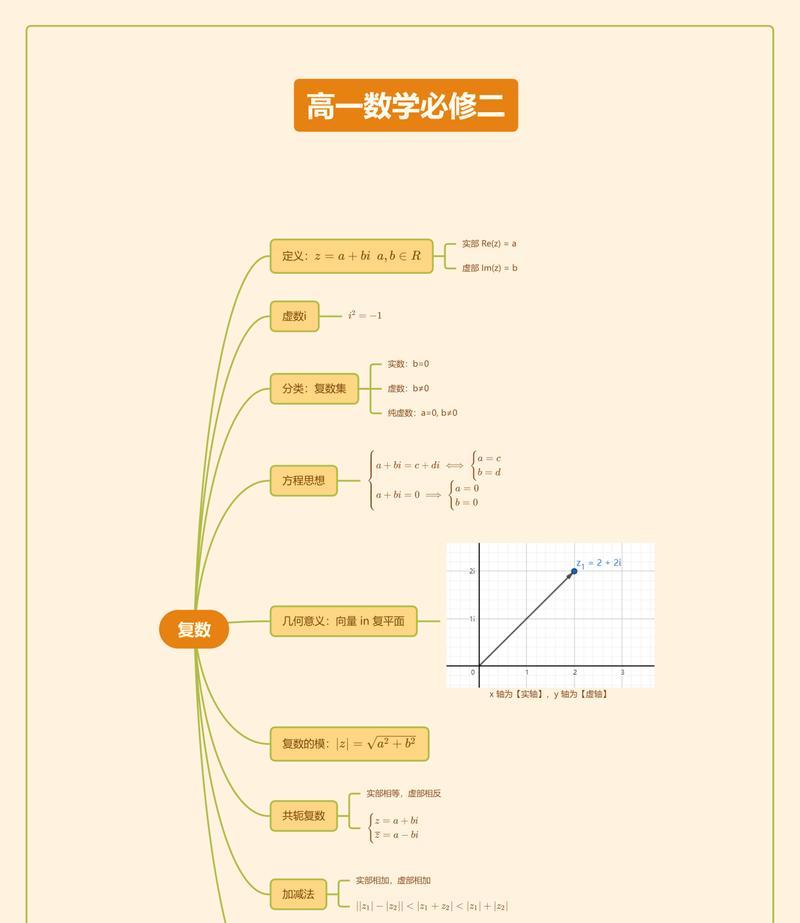
虚数的定义及基本性质

1.1虚数i的定义及数学性质

虚数i定义为平方根-1，它满足i2=-1，是一个非实数。

1.2虚数的性质及运算法则

虚数具有与实数相似的加法、减法和乘法运算法则，但除法运算则需要通过共轭复数进行转换。

复数及虚数的表示形式

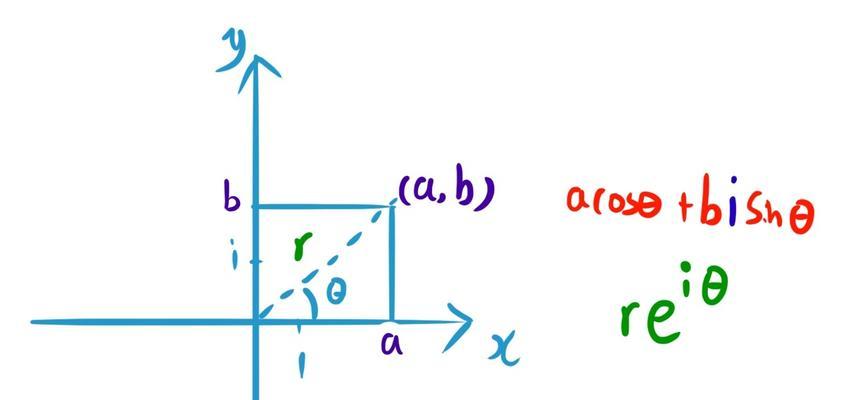
2.1复数的表示形式：直角坐标形式和极坐标形式

复数可以通过直角坐标形式表示为a+bi，也可以通过极坐标形式表示为r(cosθ+isinθ)。

2.2虚数在复平面中的表示及几何解释

虚数可以在复平面上表示为一个沿虚数轴向上延伸的点，可以通过复平面对复数进行几何解释。

虚数的运算公式及应用

3.1虚数的加法和减法运算公式

虚数的加法运算公式为(a+bi)+(c+di)=(a+c)+(b+d)i，减法运算公式为(a+bi)-(c+di)=(a-c)+(b-d)i。

3.2虚数的乘法和除法运算公式

虚数的乘法运算公式为(a+bi)(c+di)=(ac-bd)+(ad+bc)i，除法运算公式为(a+bi)/(c+di)=(ac+bd)/(c2+d2)+(bc-ad)/(c2+d2)i。

3.3虚数的幂运算公式及应用

虚数的幂运算公式为i的整数幂为周期性循环，其中i?=1，i1=i，i2=-1，i3=-i，i?=1，依此类推。

3.4虚数在电路分析中的应用

虚数在电路分析中有广泛的应用，特别是在交流电路中，通过虚数可以方便地表示电流和电压之间的相位关系。

虚数的实际应用领域

4.1虚数在物理学中的应用

虚数在物理学中的应用包括量子力学、波动光学、电磁场等领域，通过虚数可以更好地描述物理现象。

4.2虚数在工程领域中的应用

虚数在工程领域中的应用包括信号处理、控制系统、电力系统等，通过虚数可以简化计算和分析复杂的工程问题。

4.3虚数在金融领域中的应用

虚数在金融领域中的应用主要涉及到金融衍生品的定价和风险管理，通过虚数可以更准确地计算金融产品的价格和风险。

4.4虚数在计算机科学中的应用

虚数在计算机科学中的应用包括图像处理、信号处理、密码学等，通过虚数可以进行复杂的算法设计和数据分析。

通过对虚数i的运算公式及应用领域的解析，我们可以发现虚数在数学和不同领域中都发挥着重要作用。深入理解虚数概念及其运算规则，有助于我们更好地掌握和应用相关知识，为实际问题的解决提供更多可能性。